Introduction to Signals

Why digital signal processing?

If you're working on a computer, or using a computer to manipulate your data, you're almost-certainly working with digital signals. All manipulations of the data are examples of digital signal processing (for our purpose processing of discrete-time signals as instances of digital signal processing). Examples of the use of DSP:

• Filtering: Eliminating noise from signals, such as speech signals and other audio data, astronomical data, seismic data, images.
• Synthesis and manipulation: E.g. speech synthesis, music synthesis, graphics.
• Analysis: Seismic data, atmospheric data, stock market analysis.
• Voice communication: processing, encoding and decoding for store and forward.
• Voice, audio and image coding for compression.
• Active noise cancellation: Headphones, mufflers in cars
• Image processing, computer vision
• Computer graphics
• Industrial applications: Vibration analysis, chemical analysis
• Biomed: MRI, Cat scans, imaging, assays, ECGs, EMGs etc.
• Radar, Sonar
• Seismology.

Defining Signals

What is a Signal?

A signal is a way of conveying information. Gestures, semaphores, images, sound, all can be signals.

Technically - a function of time, space, or another observation variable that conveys information

We will disitnguish 3 forms of signals:

• Continuous-Time/Analog Signal
• Discrete-Time Signal
• Digital Signal

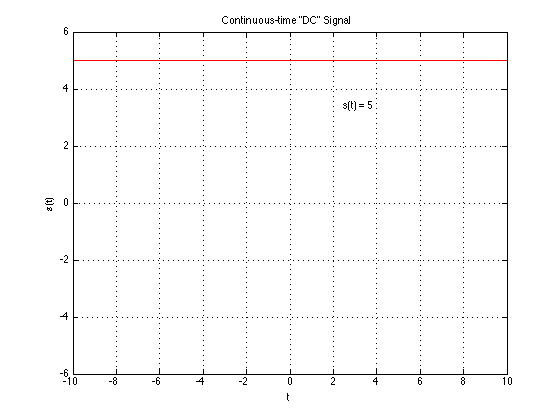
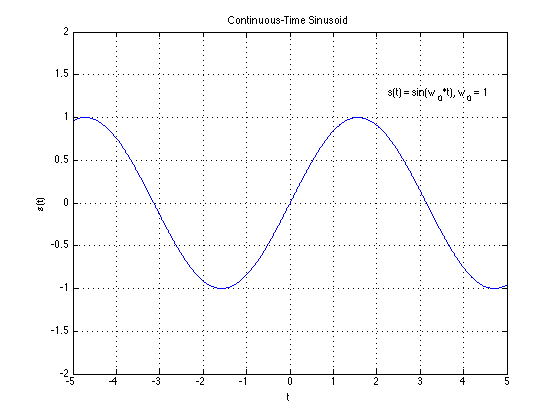
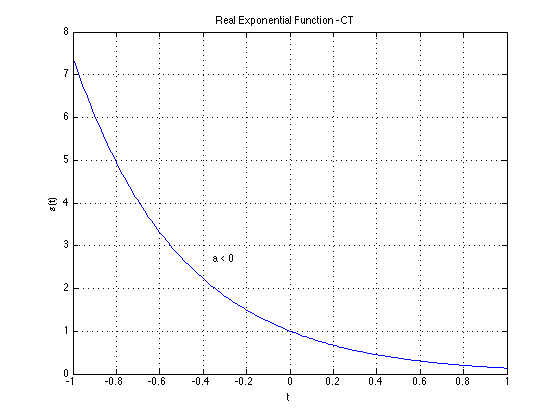
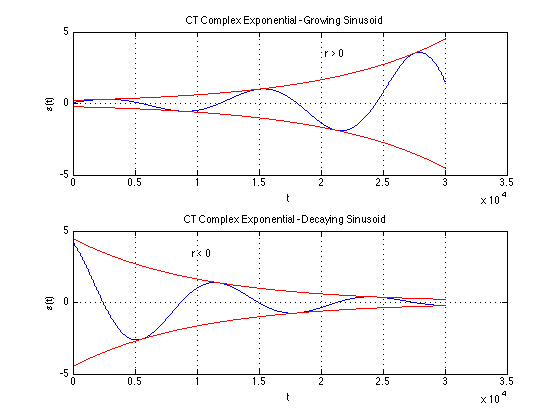
Continuous-time (CT)/Analog Signal

A finite, real-valued, smooth function $s(t)$ of a variable t which usually represents time. Both s and t in $s(t)$ are continuous

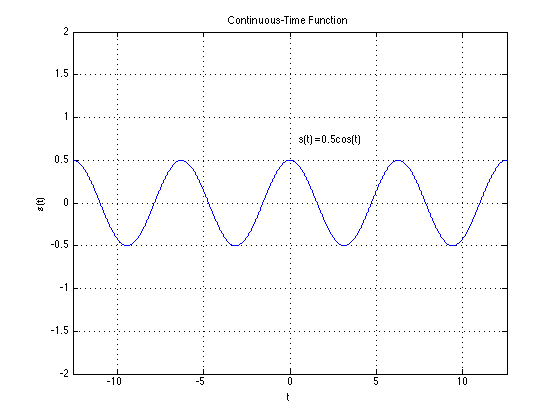
Why real-valued?

Usually real-world phenomena are real-valued.

Why finite?

Real-world signals will generally be bounded in energy, simply because there is no infinite source of energy available to us.
Alternately, particularly when they characterize long-term phenomena (e.g. radiation from the sun), they will be bounded in power.
Real-world signals will also be bounded in amplitude -- at no point will their values be infinite.

In order to claim that a signal is “finite”, we need some characterization of its “size”. To claim that the signal is finite is to claim that the size of the signal is bounded -- it never goes to infinity. Below are a few characterizations of the size of a signal. When we say that signals are finite, we imply that the size, as defined by the measurements below is finite.

1. The “energy” of a signal characterizes its “size”.

$E=\int_{-\infty}^{\infty}s^2(t)dt$

2. The "power" of a signal = energy/unit time

$P=\lim_{T \to \infty} \frac{1}{2T} \int_{-T}^{T} s^2(t)\,dt.$

3. Instantaneous power

$P_i = \lim_{\Delta t \to 0} \frac{1}{\Delta t} \int_{t}{t + \Delta t} s^2(\tau),d \tau.$

4. Amplitude = $max | s(t)|$

Why smooth?

Real world signals never change abruptly/instananeously. To be more technical, they have finite bandwidth.

Note that although we have made assumptions about signals (finiteness, real, smooth), in the actual analysis and development of signal processing techniques, these considerations are generally ignored.

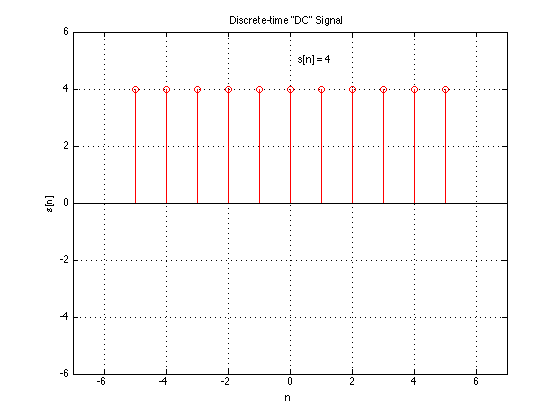
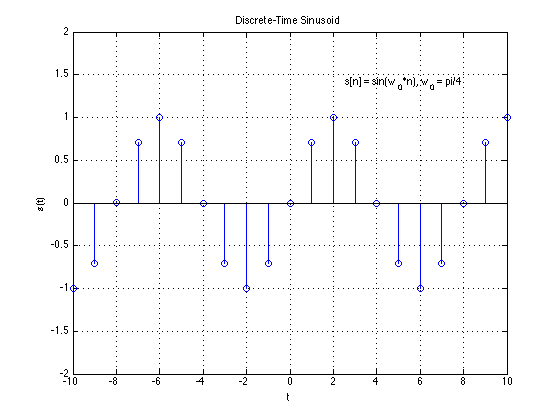
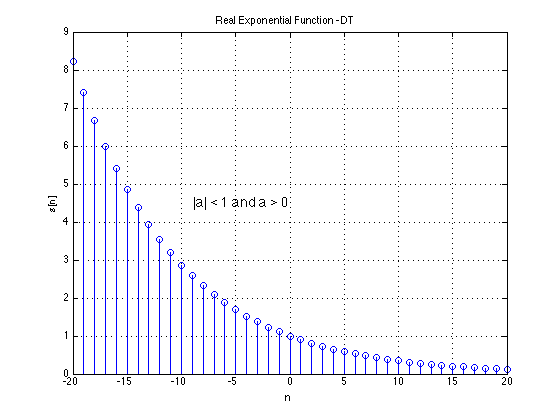
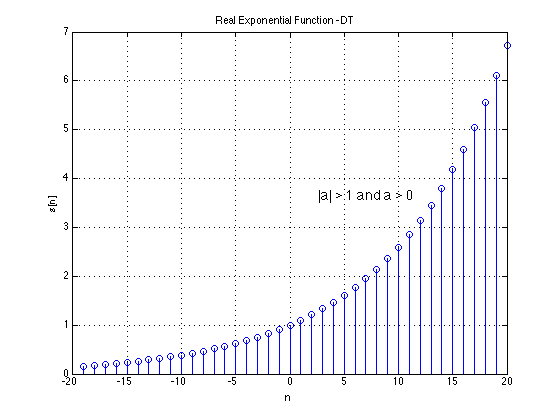
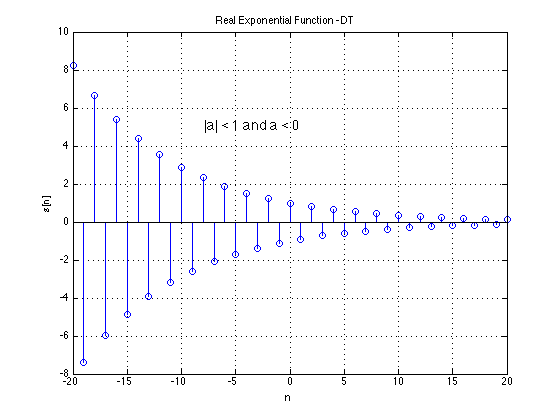
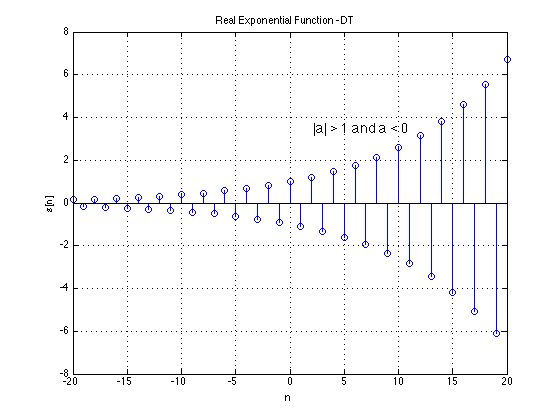
Discrete-time(DT) Signal

A discrete-time signal is a bounded, continuous-valued sequence $s[n]$. Alternately, it may be viewed as a continuous-valued function of a discrete index $n$. We often refer to the index $n$ as time, since discrete-time signals are frequently obtained by taking snapshots of a continuous-time signal as shown below. More correctly, though, $n$ is merely an index that represents sequentiality of the numbers in $s[n]$.

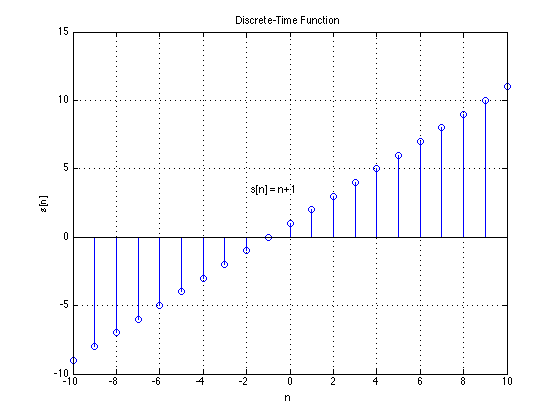
If they DT signals are snapshots of real-world signals realness and finiteness apply.

Below are several characterizations of size for a DT signal

1. Energy

$E=\sum_n s^2[n]$

2. Power

$P=\lim_{N \to \infty} \frac{1}{2N+1} \sum_{n=-N}^{N} s^2[n].$

3. Amplitude = $max | s[n]|$

Smoothness is not applicable.

Digital Signal

We will work with digital signals but develop theory mainly around discrete-time signals.

Digital computers deal with digital signals, rather than discrete-time signals. A digital signal is a sequence $s[n]$, where index the values $s[n]$ are not only finite, but can only take a finite set of values. For instance, in a digital signal, where the individual numbers $s[n]$ are stored using 16 bits integers, $s[n]$ can take one of only 2¹⁶ values.

In the digital valued series $s[n]$ the values s can only take a fixed set of values.

Digital signals are discrete-time signals obtained after "digitalization." Digital signals too are usually obtained by taking measurements from real-world phenomena. However, unlike the accepted norm for analog signals, digital signals may take complex values.

Presented above are some criteria for real-world signals. Theoretical signals are not constrained

real- this is often violated; we work with complex numbers

finite/bounded

energy - violated ALL the time

. Signals that have infinite temporal extent, i.e. which extend from $-\infty$ to $\infty$, can have infinite energy.

power - almost never: nearly all the signals we will encounter have bounded power

smoothness-- this is often violated by many of the continuous time signals we consider.

Examples of "Standard" Signals

We list some basic signal types that are frequently encountered in DSP. We list both their continuous-time and discrete-time versions. Note that the analog continuous-time versions of several of these signals are artificial constructs -- they violate some of the conditions we stated above for real-world signals and cannot actually be realized.

• The DC Signal: The “DC” or constant signal simply takes a constant value. In continuous time it would be represented as: $s(t) = 1$. In discrete time, it would be $s[n] = 1$. The number “1” may be replaced by any constant. The DC signal typically represents any constant offset from 0 in real-world signals.

  The analog DC signal has bounded amplitude and power and is smooth.

  

  

• The unit step: The “unit step”, also often referred to as a Heaviside function, is literally a step. It has 0 value until time 0, at which point, it abruptly switches to 1.0. The unit step represents events that change state, e.g. the switching on of a system, or of another signal. It is usually represented as $u(t)$ in continuous time and $u[n]$ in discrete time. \[ \text{Continuous time:}~~u(t) = \begin{cases} 0, & t < 0 \\ 1, & t > 0 \end{cases} \] \[ \text{Discrete time:}~~u[n] = \begin{cases} 0, & n < 0 \\ 1, & n \ge 0 \end{cases} \]

  

  

  In practical terms, the step function represents the switching on (or off) of a device or a signal.

  To translate the transition to time $\tau$ (N for discrete-time signal) we can write

  \[ \text{Continuous time:}~~u(t - \tau) = \begin{cases} 0, & t < \tau \\ 1, & t > \tau \end{cases} \] \[ \text{Discrete time:}~~u[n - N] = \begin{cases} 0, & n < N \\ 1, & n \ge N \end{cases} \]

  

  

  The continuous-time step function $u(t)$ violates the criterion we have stated above of smoothness, since it changes instantaneously from 0 to 1 at $t=0$. Practical realizations are only be approximations, which change value extremely quickly, but never instantaneously.
  
  
• The unit pulse: The “unit pulse” is a signal that takes the value of 1.0 for a brief period of time, and is zero everywhere else. It is often referred to by other names as well, such as the “rectangular”, or “rect” function, the “gate” function, the “Pi” function and the “boxcar” function. In particular, if you're a matlab user, you are probably familiar with the rect() and boxcar() functions. \[ \text{Continuous time:}~~rect\left(\frac{t}{T}\right) = \begin{cases} 1, & |t| < \frac{T}{2} \\ 0, & else \end{cases} \] \[ \text{Discrete time:}~~rect\left[\frac{n}{N}\right] = \begin{cases} 1, & |n| \le \frac{N}{2} \\ 0, & else \end{cases} \]

  

  

  The unit pulse is often also represented by the symbol $b$ (for boxcar), as in $b_T(t)$ and $b_N(n)$. A unit pulse typically represents a gating operation, where something is briefly switched on, and then switched off again.

  The unit pulse violates the condition of smoothness; however it does have finite energy and amplitude. Practical realizations of a pulse will have fast, but not instantaneous rising and falling edges.
  
  
  

• The pulse train: The “pulse train”, also called a “square wave” is an infinitely long train of pulses spaced equally apart in time. The pulse train is defined by: \[ \text{Continuous time:}~~p\left(t\right) = \begin{cases} 1, & t < T_1 \\ 0, & T_1 < t < T_2 \\ p(t+T_2) & {\rm in~general} \end{cases} \] \[ \text{Discrete time:}~~p\left[n\right] = \begin{cases} 1, & n < N_1 \\ 0, & N_1 \le t < N_2 \\ p[n+N_2] & {\rm in~general} \end{cases} \]

  

  

  Here $T_1$ (or $N_1$ for discrete time signals) represents the width of the pulses and $T_2$ ($N_2$ for discrete time signals) is the spacing between pulses. $T_1/T_2$ (or $N_1/N_2$ for discrete time signals) is often called the duty cycle of the square wave. Clock signals that drive computers are ideally square waves, as are various carrrier signals employed to carry information via various forms of modulation.

  The ideal pulse train violates smoothness constraints, but does have bounded amplitude and power. Practical realizations of pulse trains will have pulses with fast-rising and fast-falling edges, but the transition from 0 to 1 (and 1 to 0) will not be instantaneous.
  
  
  

• The sinusoid: The “sinusoid” is a familiar signal. \[ \text{Continuous time:}~s(t) = \cos(\omega t + \phi) \] \[ \text{Discrete time:}~s[n] = \cos(\Omega n + \phi) \]

  

  

  The sinusoid is one of the most important signals in signal processing. We will encounter it repeatedly. The continuous-time version of it shown above is a perfectly periodic signal. Note that the above equations are defined in terms of cosines. We can similarly define the sinusoid in terms of sines as $\sin(\omega t + \phi)$ and $\sin(\Omega n + \phi)$. Cosines and sines are of course related through a phase shift of $\pi/2$: $\cos(\theta) = \sin(\theta - \pi/2)$.

  The sinusoid is smooth, and has finite power and violates none of our criteria for real-world signals.

• The exponential: The “exponential” signal literally represents an exponentially increasing or falling series: \[ \text{Continuous time:}~s(t) = e^{\alpha t} \]

  

  Note that negative $\alpha$ values result in a shrinking signal, whereas positive values result in a growing signal. The exponential signal models the behavior of many phenomena, such as the decay of electrical signals across a capacitor or inductor. Positive $\alpha$ values show processes with compounding values, e.g. the growth of money with a compounded interest rate.

  The exponential signal violates boundedness, since it is infinite in value either at $t=-\infty$ (for $\alpha < 0$) or at $t = \infty$ (for $\alpha >0 $). In discrete time the definition of the exponential signal takes a slightly different form: \[ \text{Discrete time:}~s[n] = \alpha^n \] Note that although superficially similar to the continuous version, the effect of $\alpha$ on the behavior of the signal is slightly different. The sign of $\alpha$ does not affect the rising or falling of the signal; instead it affects its oscillatory behavior. Negative alphas cause the signal to alternate between negative and positive values. The magnitude of $\alpha$ affects the rising and falling behavior: $|\alpha | < 1$ results in falling signals, whereas $|\alpha| > 1$ results in rising signals.

  

  

  
  
  
  
• The complex exponential: The “complex exponential” signal is probably the second most important signal we will study. It is fundamental to many forms of signal representations and much of signal processing. The complex exponential is a complex valued signal that simultaneously encapsulates both a cosine signal and a sine signal by posting them on the real and imaginary components of the complex signal.

  The continuous-time complex exponential is defined as: \[ \text{Continuous time:}~s(t) = C e^{\alpha t} \] where $C$ and $a$ are both complex. Recall Euler's formula: $\exp(j \theta) = \cos(\theta) + j \sin(\theta)$. Any complex number $x = x_r + j x_i$ can be written as $x = |x|e^{j\phi}$, where $|x| = \sqrt{x_r^2 + x_i^2}$ and $\phi = \arctan\frac{x_i}{x_r}$. So, letting $\alpha = r + j\omega$, and $C = |C|e^{j\phi}$ in the above formula, we can write \[ \text{Continuous time:}~s(t) = |C| e^{r t}e^{j(\omega t + \phi)} = |C| e^{r t} \left(\cos(\omega t + \phi) + j \sin(\omega t + \phi)\right) \]

  

  Clearly, the complex exponential, comprising complex values, does not satifsy our requirement for real-world signals that they be real-valued. Moreover, for $r \neq 0$, the signal is not bounded either.

  The discrete-time complex exponential follows the general definitionof the discrete-time real exponential: \[ \text{Discrete time:}~s[n] = C\alpha^n \] where $C$ and $\alpha$ are complex. Expressing the complex numbers in terms of their magnitude and angle as $C = |C|e^{j\phi}$ and $\alpha = |\alpha|e^{j\omega}$, we can express the discrete-time complex exponential as: \[ \text{Discrete time:}~s[n] = |C||\alpha|^n \exp\left(j(\omega n + \phi)\right) = |C||\alpha|^n \left(\cos(\omega n + \phi) + j \sin(\omega n + \phi)\right) \]

  

  
  
  
  
• The impulse function: The “impulse function”, also known as the delta function, is possibly the most important signal to know about in signal processing. It is important enough to require a special section of its own in these notes. Technically, it is a signal of unit energy, that takes non-zero values at exactly one instant of time, and is zero everywhere else.

  The continuous-time (analog) version of the delta function is the Dirac delta. Briefly, but somewhat non-rigorously, we can define the Dirac delta as follows: \[ \delta(t) = \begin{cases} \infty & t = 0 \\ 0, & t \neq 0 \end{cases} \] \[ \int^\infty_{-\infty} \delta(t) dt = 1.0 \] The above definition states that the impulse function is zero everywhere except at $t=0$, and the area under the function is 1.0. Technically, the impulse function is not a true function at all, and the above definition is imprecise. If one must be precise, the impulse function is defined only through its integral, and its properties. Specifically, in addition to the property $\int^\infty_{-\infty} \delta(t) dt = 1.0$, it has the property that for any function $x(t)$ which is bounded in value at $t=0$, \[ \int^\infty_{-\infty} x(t) \delta(t) dt = x(0) \]

  

  Note that the Dirac delta function itself is not smooth and is unbounded in amplitude.

  The discrete-time version of the delta function is the Kronecker delta. It is precisely defined as \[ \delta[n] = \begin{cases} 1 & n = 0 \\ 0, & n \neq 0 \end{cases} \]

  

  Note that naturally also satisifies

  $\sum_{n=-\infty}^{\infty} \delta[n] = 1$ and $\sum_{n=-\infty}^{\infty} x[n]\delta[n] = x[0]$.

Signal Types

We can categorize signals by their properties, all of which will affect our analysis of these signals later.

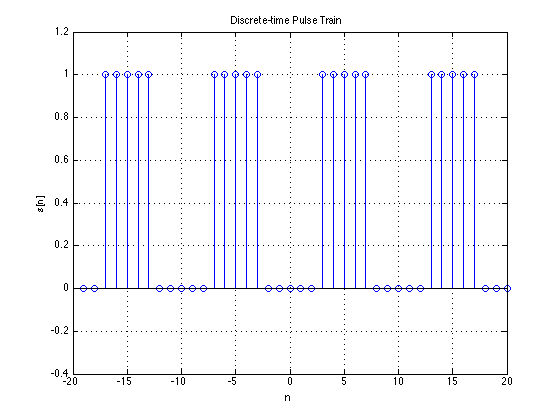
Periodic signals

A signal is periodic if it repeats itself exactly after some period of time. The connotations of periodicity, however, differ for continuous-time and discrete time signals. We will deal with each of these in turn.

Continuous Time Signals Thus, in continous time a signal if said to be periodic if there exists any value $T$ such that \[ s(t) = s(t + MT),~~~~~ -\infty\leq M \leq \infty,~~\text{integer}~M \] The smallest $T$ for which the above relation holds the period of the signal.

Discrete Time Signals

The definition of periodicity in discrete-time signals is analogous to that for continuous time signals, with one key difference: the period must be an integer. This leads to some non-intuitive conclusions as we shall see.

A discrete time signal $x[n]$ is said to be periodic if there is a positive integer value $N$ such that \[ x[n] = x[n + MN] \] for all integer $M$. The smallest $N$ for which the above holds is the period of the signal.

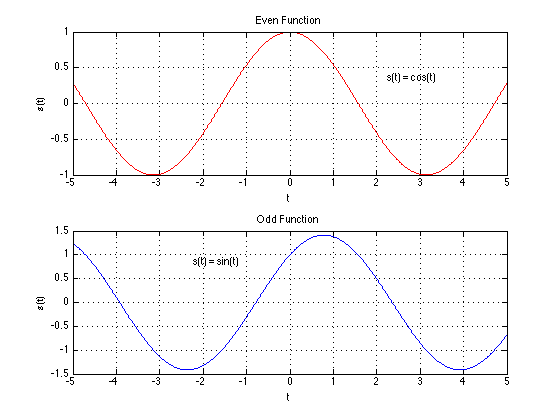
Even and odd signals

An even symmetic signal is a signal that is mirror reflected at time $t=0$. A signal is even if it has the following property: \[ \text{Continuous time:}~s(t) = s(-t) \\ \text{Discrete time:}~s[n] = s[-n] \]

A signal is odd symmetic signal if it has the following property: \[ \text{Continuous time:}~s(t) = -s(-t) \\ \text{Discrete time:}~s[n] = -s[-n] \]

The figure below shows examples of even and odd symmetric signals. As an example, the cosine is even symmetric, since $\cos(\theta) = \cos(-\theta)$, leading to $\cos(\omega t) = \cos(\omega(-t))$. On the other hand the sine is odd symmetric, since $\sin(\theta) = -\sin(-\theta)$, leading to $\sin(\omega t) = -\sin(\omega(-t))$.

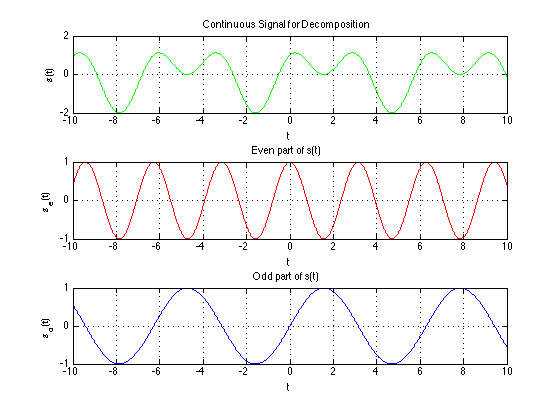
Decomposing a signal into even and odd components Any signal $x[n]$ can be expressed as the sum of an even signal and an odd signal, as follows \[ x[n] = x_{even}[n] + x_{odd}[n] \] where \[ x_{even}[n] = 0.5(x[n] + x[-n]) \\ x_{odd}[n] = 0.5(x[n] - x[-n]) \]

Manipulating signals

Signals can be composed by manipulating and combining other signals. We will consider these manipulations briefly.

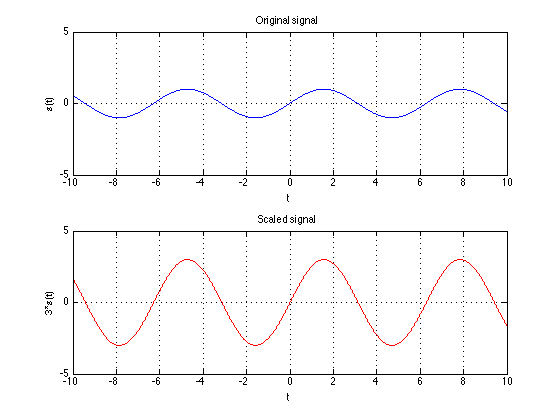
Scaling

Simply scaling a signal up or down by a gain term.

Continuous time: $y(t)= a x(t)$

Discrete time: $y[n]= a x[n]$

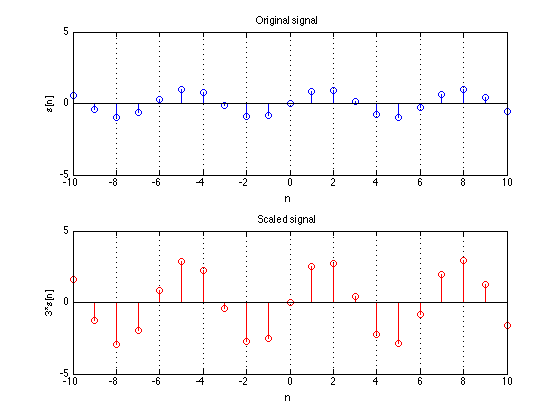
$a$ can be a real/imaginary, positive/negative. When $a is negative, the signal is flipped across the y-axis.

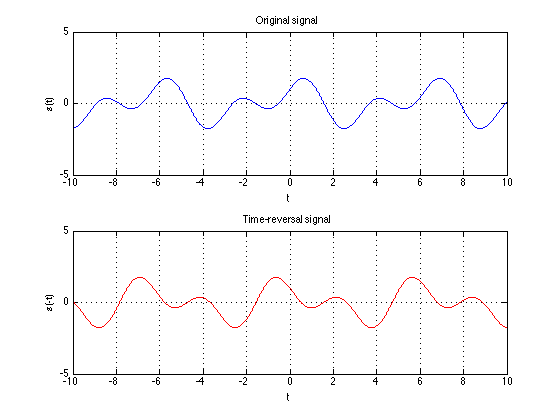
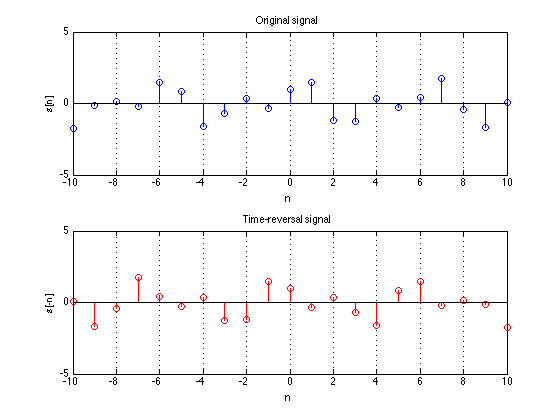
Time reversal

Flipping a signal left to right.

Continuous time: $y(t) = x(-t)$

Discrete time: $y[n] = x[-n]$

Time shift

The signal is displaced along the indendent axis by $\tau$ (or N for discrete time). If $\tau$ is positive, the signal is delayed and if $\tau$ is negative the signal is advanced.

Continuous time: $y(t) = x(t- \tau)$

Discrete time: $y[n] = x[n - N]$

Dilation

The time axis itself can scaled by $\alpha$.

Continuous time: $y(t) = x(\alpha t)$

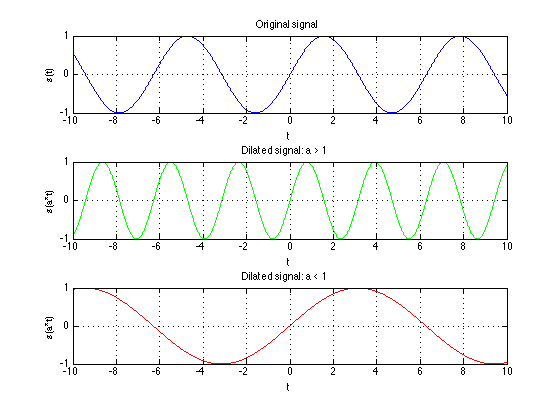
Discrete time: $y[n] = x[/alpha n]$

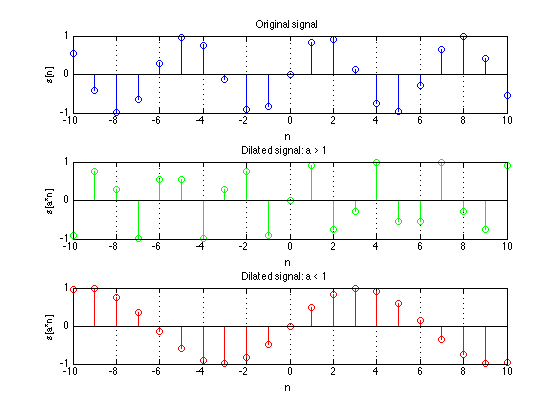
The DT dilation differs from CT dilation because $x[n]$ is ONLY defined at integer n so for $y[n] = x[\alpha n]$ to exist "an" must be an integer.

However $x[\alpha n]$ for $a \neq 1$ loses some samples. You can never recover x[n] fully from it. This process is often called decimincation.

For DT signals $y[n] = x[\alpha n]$ for $\alpha < 1$ does not exist. Why? y[0] = x[0] OK y[1] = x[\alpha] If $a < 1$ this does not exist. Instead we must interpolate zeros for undefined valued if $an$ is not an integer.

Composing Signals

Signals can be composed by manipuating and combining other signals There are may ways of combining signals and we consider the following two:

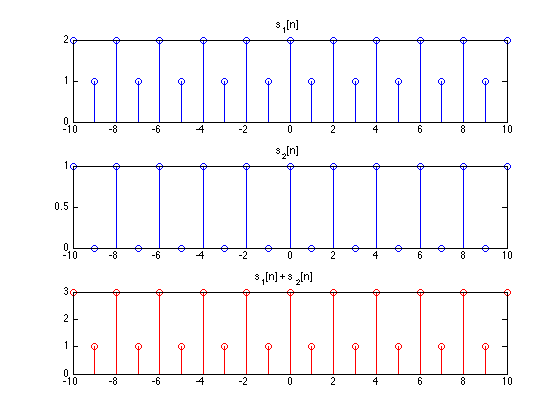
ADDITION

Continuous-time: $y(t) = x_1(t) + x_2(t)$ Discrete-time: $y[n] = x_1[n] + x_2[n]$

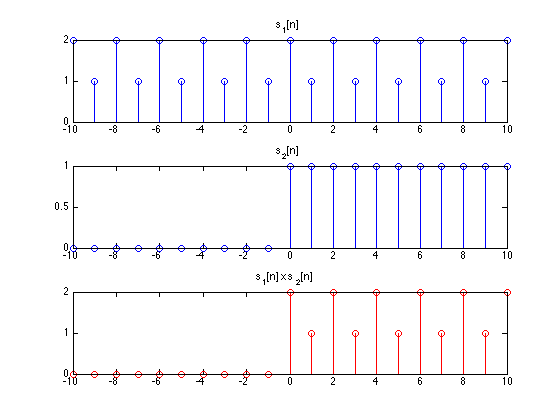
MULTIPLICATION

Continuous-time:   $y(t) = x_1(t) x_2(t)$ Discrete-time:    $y[n] = y_1[n] y_2[n]$

$x_1[n]$ and $x_2[n]$ can themselves be ontained by manipulating other signals. For exmple below we have a truncated expontential begins at t=0.

This signal can be obtained by multiplying

$x_1(t) = e^{\alpha t}$ and $x_2(t) = u(t)$

where $y(t) = e^{\alpha t} u(t)$ for $\alpha < 0$. Same is true for discrete time signals. In genral one-sided signals can be obtained by multiplying by u[n] (or shifted/time-reversed versions of u[n] or u(t))

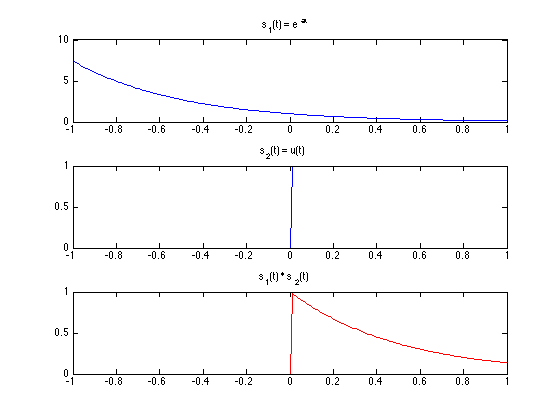
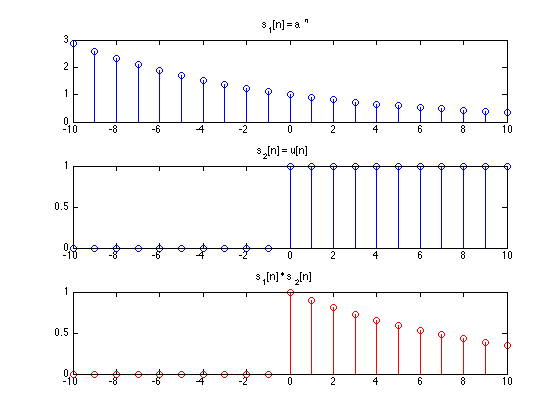
In gernal one-sided signals can be obtained by multiplying by u[n] (or shifted/time-reversed versions of u[n] or u(t)).

Deriving Basic Signals from One Another

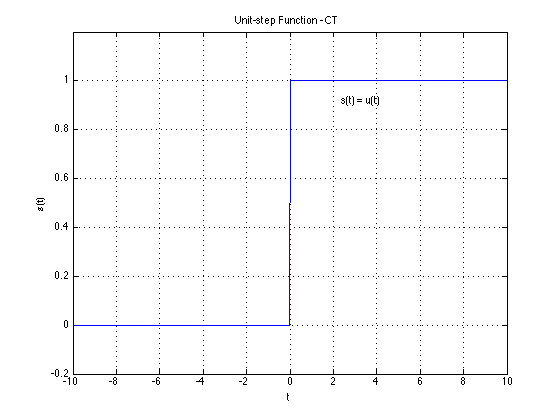
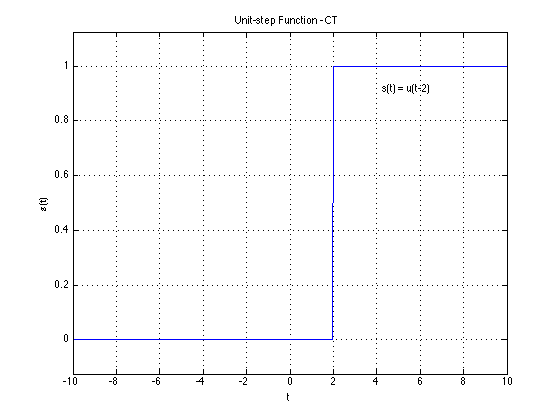
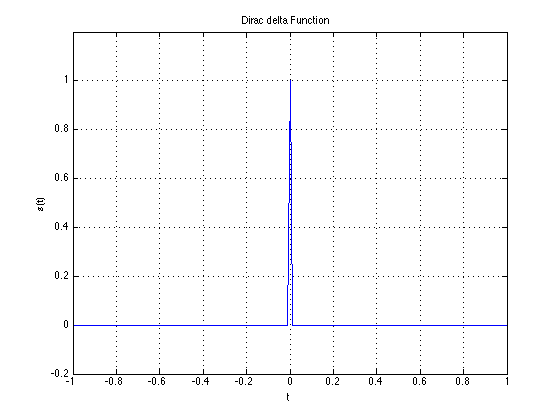
It is possible to derive one signal from another simply through mathematical manipulation. Remember in continuous-time; $u(t)$ and $\delta(t)$

$\delta(t) = \frac{du(t)}{dt}$

$u(t) = \int_{-\infty}^{t} \delta (\tau) d\tau$

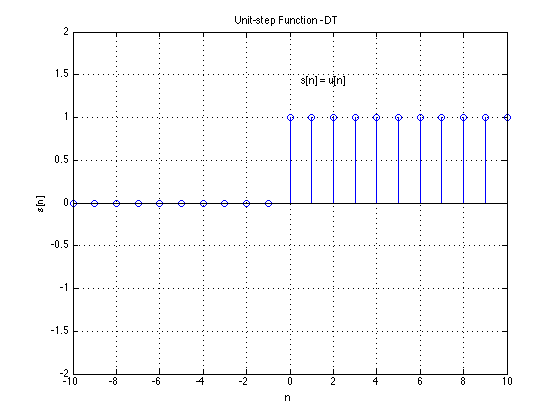
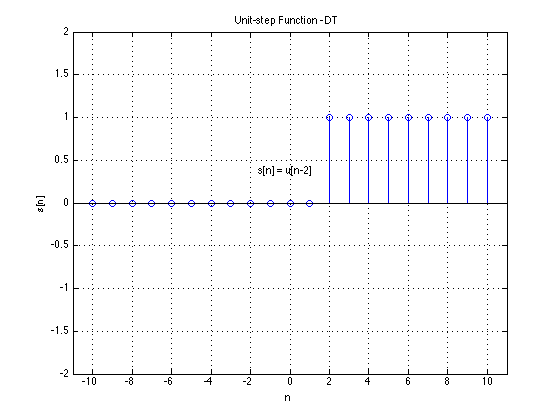
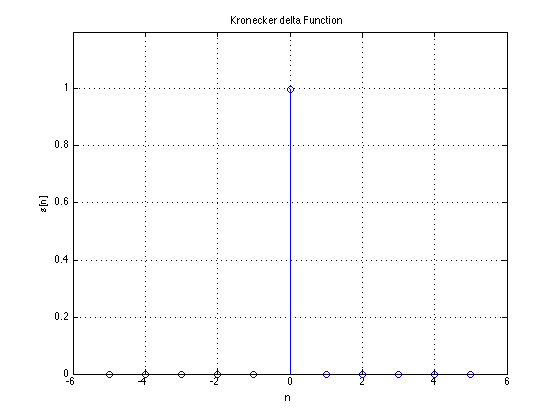
In discrete-time: $u[n]$ and $\delta[n]$

So

$\delta[n] = u[n] - u[n-1]$

$\delta[n] = u[n] - u[n-k]$ and $u[n] = \sum_{k=\infty}^{n} \delta[k]$

Another way of defining $u[n]$ is

$u[n] = \sum_{k=0}^{\infty}\delta[n-k]$

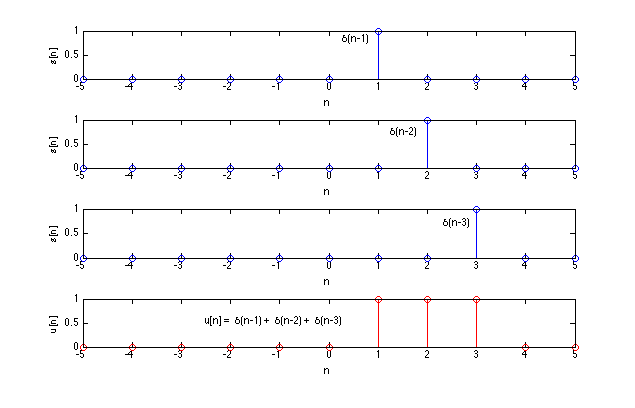
In general:

$u[n] = \sum_{k= -\infty}^{\infty} u[k]\delta[n-k]$