Homework 1A
In this homework we will exercise some basic concepts. All problems relate to discrete-time signals unless otherwise specified.
I. Composing signals.
We have considered several signals in class:
- The DC “signal”: $s[n] = 1$
- The unit step: $u[n] = 1$ for $n \ge 0$, and $0$ elsewhere.
- The unit pulse: $p_N[n] = 1$ for $0 \le n < N$, and 0 elsewhere. The parameter for the unit pulse is the width, $N$.
- The sinusoid: $s_{\omega,\phi}[n] = \sin(\omega n + \phi)$. The parameters of the sinusoid are the frequency $\omega$ and phase, $\phi$.
- The exponential: $e_\alpha[n] = \alpha^n$. The parameter is $\alpha$.
- The complex exponential: $e_{\omega,\phi}[n] = e^{j(\omega n + \phi)}$. The parameters of the complex exponential are the frequency $\omega$ and phase, $\phi$.
- The kronecker delta: $\delta[n] = 1$ at $n=0$ and $0$ elsewhere.
We have also noted that signals can be manipulated in many ways:
- Scaling: $y[n] = \alpha s[n]$
- Shift: $y[n] = s[n-n_0]$
- Time reversal: $y[n] = s[-n]$
- Time dilation: $y[n] = s[\alpha n]$
Signals can also be combined in various ways, e.g.
- Addition: $y[n] = s_1[n] + s_2[n]$
- Multiplication: $y[n] = s_1[n] s_2[n]$
Using the basic signals, operations and combination methods mentioned above, compose the following signals.
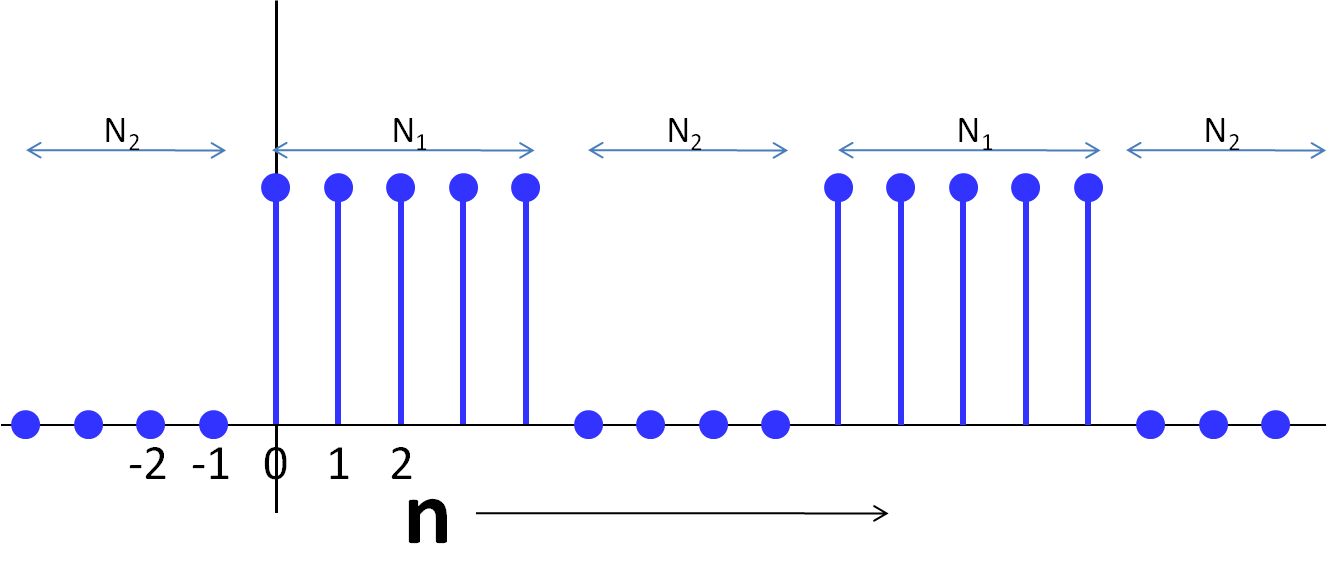
- A pulse train, where each pulse has width $N_1$, and the gap between pulses is $N_2$.
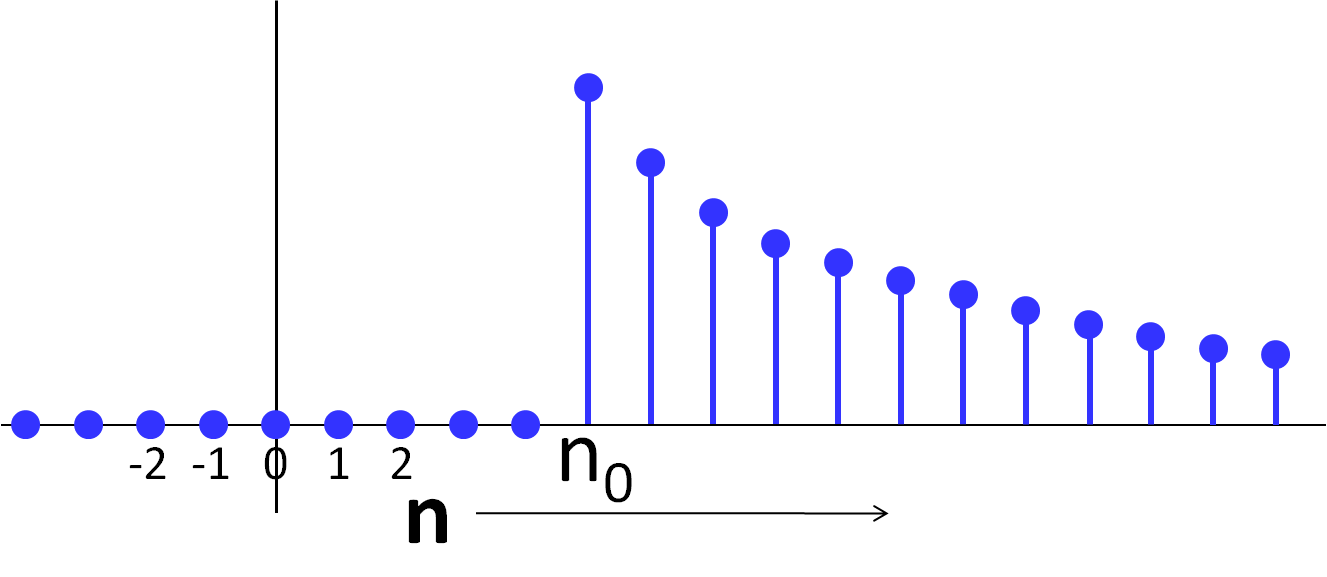
- An exponential signal that begins at $n=n_0$ and tapers thereafter as $\alpha^{n-n_0}$.
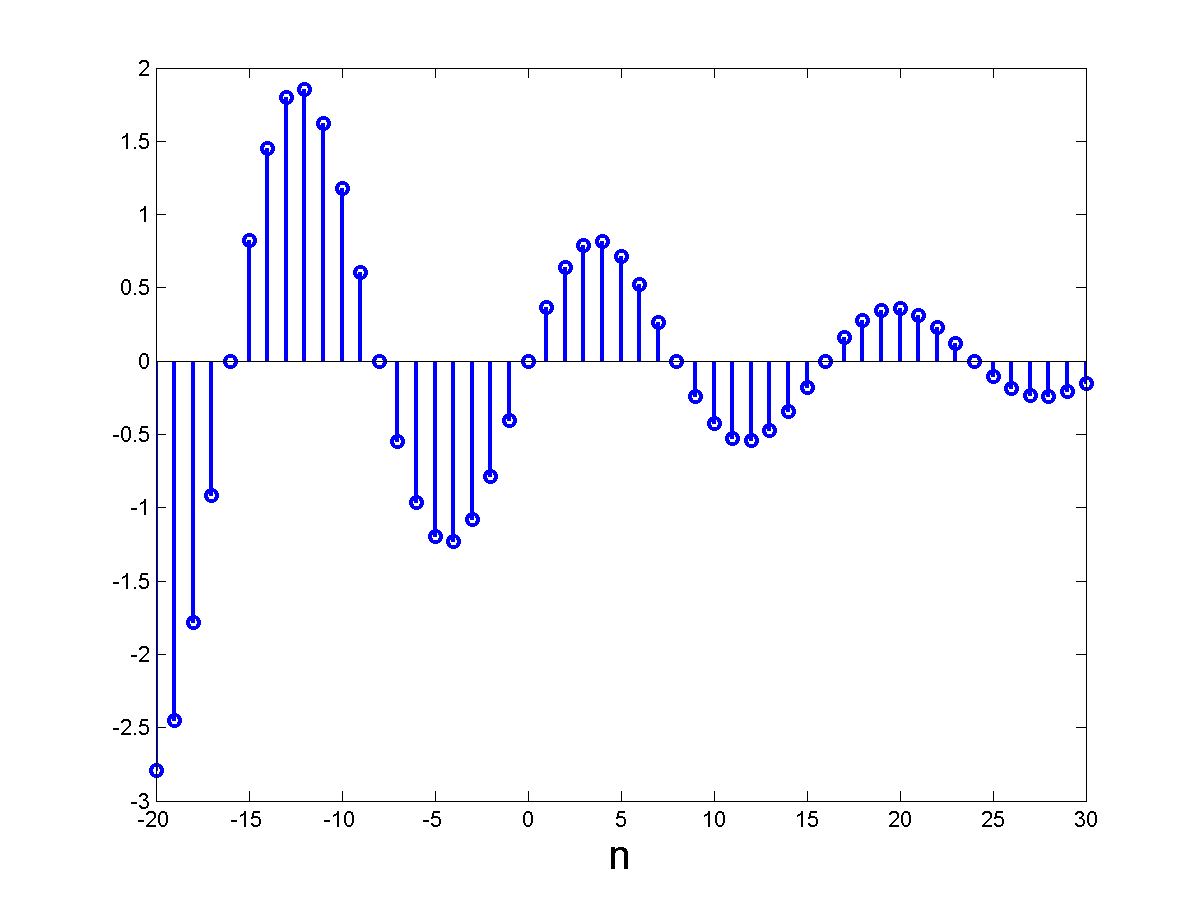
- An sine wave (with zero phase) whose amplitude falls off exponentially as $\alpha^n$.
- A complex exponential of frequency $\omega$ and zero phase, which ends abruptly at $n=-n_0$.
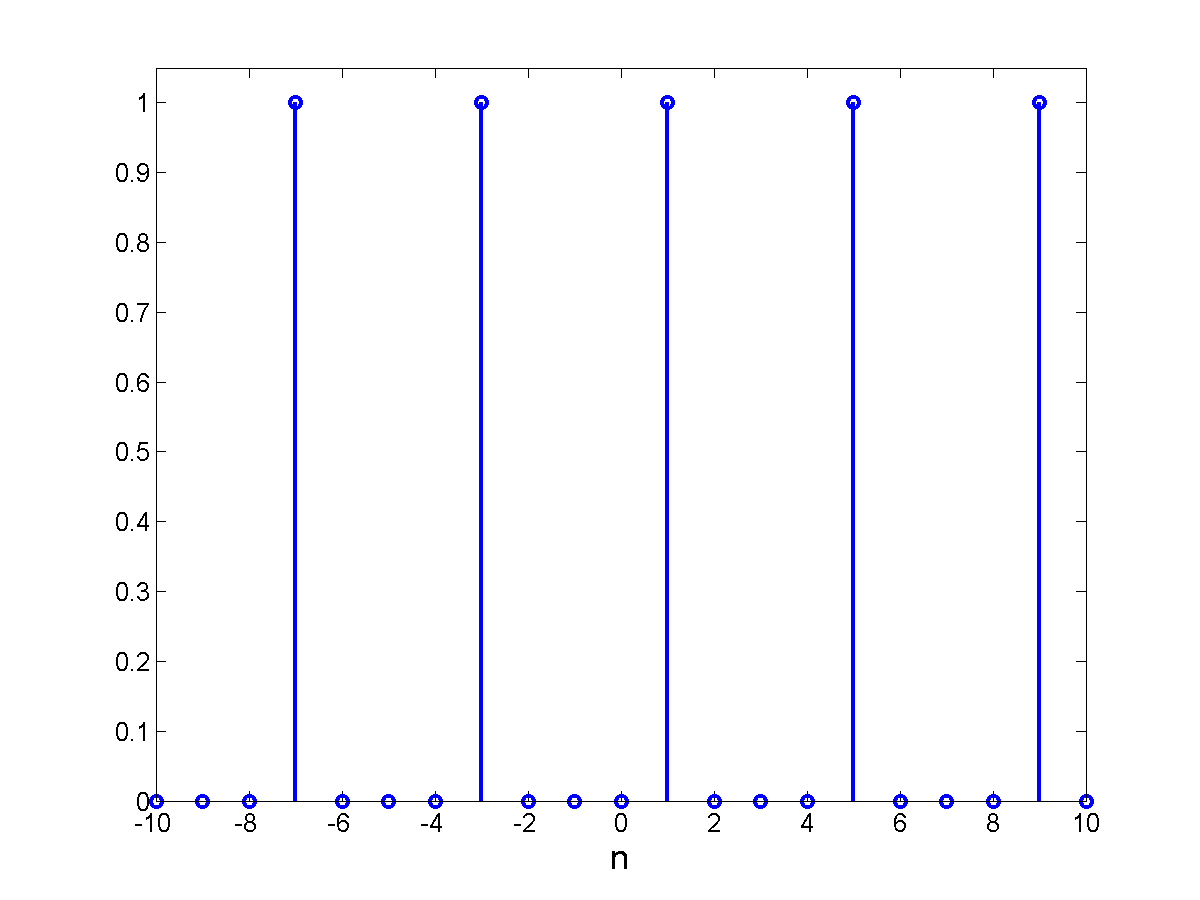
- A impulse train with impulses at $n = ...-7,-3,1,5,9,..$ (i.e. with a spacing of 4).
II. System properties
The equations below define several systems. Please state if these systems are
- Causal
- Memoryless
- Linear
- Shift invariant
Explain why you arrived at your conclusions. If you can also hypothesize whether the systems are invertible, and explain why they are or not invertible, you get bonus points.
- $y[n] = \alpha x[n-4]$
- $y[n] = \alpha_0 x[n] + \alpha_1 x[n+1]$
- $y[n] = \alpha_0 x[n] + \alpha_1 x[n-1] + \beta_1 y[n-1]$
- $y[n] = \sum_{k=-K}^0 n x[n-k]$
- $y[n] = \sum_{k=-K}^0 k x[n-k]$
- $y[n] = x^4[n]$
Due date: Tuesday, 10th Feb







